Boost Graph LibraryとGraphvizでグラフの可視化
グラフの可視化
BGLとGraphvizを用いてグラフを可視化します.
Boost Graph Library: write graphviz - 1.61.0
を参考にしました.
macの場合,Graphvizのinstallはbrewで簡単に行うことができます(それ以外の方法は調査していません..).
brew install graphviz
また,boostのinstallもbrewで同様に実行可能です.
brew install boost
ソースコード
#include <fstream>
#include <string>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/graphviz.hpp>
int main()
{
boost::adjacency_list<> g;
std::string labels = "R1234";
auto root = boost::add_vertex(g);
auto node1 = boost::add_vertex(g);
auto node2 = boost::add_vertex(g);
auto node3 = boost::add_vertex(g);
auto node4 = boost::add_vertex(g);
boost::add_edge(root, node1, g);
boost::add_edge(root, node2, g);
boost::add_edge(node1, node3, g);
boost::add_edge(node2, node4, g);
std::ofstream file("test.dot");
boost::write_graphviz(file, g, boost::make_label_writer(labels.c_str()));
}
まずはじめに,5つのノードと4つのエッジをもつグラフgを構築します.
これはBGLを用いて簡単に行うことができます.
つぎに,write_graphviz()という関数でdotファイルを作成し,これをもとにpngファイルを生成します.
write_graphviz()の出力先はofstreamで指定しています.
dotファイルの中身は次のようになります.
digraph G {
0[label=R];
1[label=1];
2[label=2];
3[label=3];
4[label=4];
0->1 ;
0->2 ;
1->3 ;
2->4 ;
}
第3引数のmake_label_writer()はノードのラベルを貼る関数です.
これを引数に渡すことで,ノードにラベルが貼られた状態でpngファイルが生成されます.
さいごに,dotコマンドによってpngファイルを生成します.
dot -Tpng test.dot -o test.png
結果として,以下の画像が生成されました.
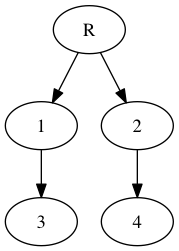
ラベルが付与されているのがわかります.
まとめ
BGLとGraphvizを用いることで,簡単にグラフを可視化することができました.
構築したグラフの形状をコードを眺めるだけで理解することは難しいので,このように楽に可視化できればとても便利です.
Boost Graph Libraryメモ②
Boost Graph Library (BGL)
1つ前の記事
でBGLについて少し触れた.
この記事では隣接行列の形でグラフを表現するadjacency_matrixを紹介する.
上の記事で紹介したadjacency_listクラスは,隣接リストグラフ構造を表現するために使用するインターフェースである.
adjacency_matrix
adjacency_matrix<Directed, VertexProperty, EdgeProperty, GraphProperty, Allocator>
adjacency_matrixの利点としては,辺の削除や追加が定数時間で終了するという点が挙げられる.
しかし,行列はn×nであり,メモリ消費量が大きいという欠点がある(nはノード数とする).
adjacency_matrixはグラフの密度が高い(辺の本数が多い)場合に向いていて,adjacency_listは密度が低い場合に向いている.
パラメータ
adjacency_matrixにはDirected, VertexProperty, EdgeProperty, GraphProperty, Allocatorという5つのパラメータが存在する.
Directedは有向か無向かを決定し,VertexProperty,EdgeProperty,GraphPropertyはプロパティを設定する.
Allocatorには特に記述がなかったが,おそらくメモリの確保や割り当てを行うオブジェクトのことを意味していると思う.
使用例
例が紹介されていた.
enum { A, B, C, D, E, F, N };
const char* name = "ABCDEF";
typedef boost::adjacency_matrix<boost::directedS> Graph;
Graph g(N);
add_edge(B, C, g);
add_edge(B, F, g);
add_edge(C, A, g);
add_edge(C, C, g);
add_edge(D, E, g);
add_edge(E, D, g);
add_edge(F, A, g);
std::cout << "vertex set: ";
boost::print_vertices(g, name);
std::cout << std::endl;
std::cout << "edge set: ";
boost::print_edges(g, name);
std::cout << std::endl;
std::cout << "out-edges: " << std::endl;
boost::print_graph(g, name);
std::cout << std::endl;
The output is:
vertex set: A B C D E F
edge set: (B,C) (B,F) (C,A) (C,C) (D,E) (E,D) (F,A)
out-edges:
A -->
B --> C F
C --> A C
D --> E
E --> D
F --> A
addEdge()で辺を追加し,boost::print_graph()でedge setを出力する.
他にもnum_vertices()で頂点数を,num_edges()で辺の数を得る関数などが用意されている.
さいごに
今後もBGLを使用したプログラムの例などを記事にしたいと思います.PageRank計算を行うプログラムなど,具体的な例を紹介できればと思います.
Boost Graph Libraryメモ
Boost Graph Library (BGL)
C++でグラフを扱うプログラムを作成するために,BGLの勉強を始める. Table of Contents: Boost Graph Libraryを参考にする.
BGLはグラフの構造へどのようにアクセスするかを定めた インタフェースである。グラフ構造はadjacency_listクラスで実装する.
adjacency_list
adjacency_listの詳細は
Boost Graph Library: Adjacency List
に,使い方は
に詳しい記述がある.
adjacency_list<EdgeList, VertexList, Directed, VertexProperties, EdgeProperties, GraphProperties>
- EdgeList, VertexListはそれぞれどの種類のコンテナを用いて辺と頂点を表現するかを決定する.
std::vectorを使用する場合はvecS,std::listを使用する場合はlistSを選択する.
- Directedは有向か無向か,または双方向の辺アクセス (出辺と入辺の両方にアクセス する) の有向かを選ぶ.
有向グラフを選ぶには directedS か bidirectionalS を使い、無向グラフを選ぶには undirectedS を使う。
あとの3つはプロパティを設定する.
それぞれデフォルトはvecS,vecS,directedS,no_property,no_property,no_propertyである.
使用例
family treeをグラフで表現した例が以下に挙げられていた.
http://boost.cppll.jp/HEAD/libs/graph/example/family-tree-eg.cpp
後日実際に実装して新たに記事にしたい.
追記 (2016/6/22)
とても分かりやすいスライドを見つけました.
www.slideshare.net
BGLについて学びたい方にとてもオススメです.
Efficient Ad-hoc Search for Personalized PageRank [SIGMOD'13]
Ad-hocにPersonalized PageRankを計算
グラフはdynamicに変化するため,ad-hocに検索する手法が重要.
この論文は,前処理することなくPersonalized PageRankのtop-kを高速かつ正確に計算する.
問題
Given: Graph G, the scaling parameter c, required number of answer nodes k, and set of query nodes Q.
Find: Top-k nodes exactly where k nodes are arranged in descending order with respect to their PPR scores.
提案手法
アイデア
反復計算の各ステップにおいて,
最終的なスコアの上限と下限の推定値をそれぞれ計算する.
推定値に基づき,不必要なノードを取り除いた部分グラフを構築.
グラフ全体ではなく,部分グラフに対してのみスコアを計算.
詳細
k-th highest lower estimationをεkとしたとき,upper estimationがεkよりも小さいノードは解になり得ない.
部分グラフは,解になり得るノードと,それにi hopで到達可能なノードの集合とする.
実験
Norredame, CNR, Email, Socialの4つのデータセットを使用.
実行速度
それぞれ90%, 75%, 85%, 65%ほど削減できた.
ノード数が同程度の場合でも,グラフの直径によって実行速度は異なる.
正確性
- 得られる結果は,オリジナルの手法の結果と一致する.
Flexibility
- scaling parameterが小さいほど高速
推定値がより正確になるため
Case-Studies
航空データを使用したcase studyが紹介されていた.
- scaling parameterが小さいほど,locally-orientedとなった.
最初はc=0.5に設定し,locally-orientedにしたいなら値を小さくする.そうでないなら値を大きくするのが推奨されていた.
Efficient Personalized PageRank with Accuracy Assurance [KDD'12]
Personalized PageRank (PPR) の効率的な計算
この論文は,Personalized PageRankの3つの問題を効率的に計算する手法を提案した.
QR分解あたりの証明が難しく,あとで再確認する.
問題
Problem1 (Single-node relevance computation)
Given: Query node x and query distribution d.
Find: Relevance score of node x according to query distribution d.
Problem2 (Top-k nodes identification)
Given: The number of required answer nodes, K, and query distribution d.
Find: Top K nodes with the highest relevance scores with respect to query distribution d.
Problem3 (Highly relevant node detection)
Given: The threshold, ε, and query distribution d.
Find: Nodes whose relevance scores are higher than ε with respect to query distribution d.
提案手法
アイデア
ベクトルの内積によってsingle node scoreを計算.(Problem1)
最終的なスコアの下限値と上限値を推定し,解になり得るかどうかを判定する.(Problem2, 3)
詳細
Problem1
Problem2, 3
はじめに全てのノードの下限値を推定.
下限値の降順でノードをたどる.
解になり得ないノードに到達したとき,処理を終了する.
Problem2, 3でノードのスコアが必要になったとき,Problem1のsingle node score計算を利用している.
(説明が雑なので,あとでノートで確認する...)
実験
Table2より,Q,Rが確かに疎になっていることが確認できる.
すべての問題について,良い性能を示した.
Case-Studies
航空データを用いたcase studyが紹介されている.
San Diego, New York, Denver, Orlandoをseed nodeとして,関連の強い都市を検出した.